Converting between Miller Indices and Spherical Coordinates

Steven Dutch, Professor Emeritus, Natural and Applied Sciences, Universityof Wisconsin - Green Bay

---

This is very basic to crystallography, so basic that textbooks don't include it much, figuring it's either in some other reference or it's programmed into the computer that analyzes the x-ray data. Except that the old references that once had all the formulas seem to get discarded. The simplest case involves the three systems with mutually orthogonal edges, and it gets progressively uglier from there.

Orthorhombic, Tetragonal and Isometric systems

The three systems with orthogonal cell edges are simplest because the cell edges line up with the Cartesian axes If a face has Miller Indices [hkl] and the cell edges are a, b, and c, then the Cartesian intercepts of the face are a/h, b/k and c/l (note that's lower case "L", not 1). In terms of cells, the intercepts are proportional to 1/h, 1/k and 1/l, but in terms of actual physical dimension, each intercept has to be multiplied by the respective edge length.

In the view at left, looking down the z-axis, we can see clearly that tan(theta) = (a/h)/(b/k) = ak/bh. Also note that p = (a/h)cos(theta). The view at right is the vertical plane normal to hkl and containing the z axis. Clearly tan(phi) = c/pl = c/(l(a/h)cos(theta)) = ch/(al*cos(theta)) = ck/(bl*sin(theta))

Wait, what? Phi and theta are independent variables. So why does theta appear in the formula for phi? Phi and theta are independent but both phi and theta determine the intercepts. We could use the fact that
tan(theta) = ak/bh to write a formula for sin(theta), but this approach is a lot cleaner. (The phi-free formula is tan(phi) = (c/l)√((h/a)² + (b/k)²), in case you're curious.)

Thus:      tan theta = ak/bh    tan(phi) = ch/(al*cos(theta)) = (c/l)√((h/a)² + (b/k)²)

In the inverse direction, the direction cosines for a line with spherical coordinates (phi, theta) are
cx =sin(phi)cos(theta),  cy = sin(phi)sin(theta) and cz = cos(phi), where cx, cy, and cz are the cosines of the angles between the pole and the x, y and z axes.. Direction numbers of the plane will be h/a, k/b and l/c, which are proportional to the direction cosines. So we can writeh = a*sin(phi)cos(theta),  
k = b*sin(phi)sin(theta) and l = c*cos(phi), then reduce them to lowest terms.

Example:

Orthorhombic crystal with a = 6, b = 7.2 and c = 8 and Face [123]. Tan(theta) = 3*2/3.6*1 = 1.6667, and theta = 59.03 degrees. Tan(phi) = 8*1/(6*3 cos(59.03) = 8/(18*0.5149) = 0.8639 and phi = 40.82 degrees

In the inverse direction, given phi = 40.82 degrees and theta = 59.03 degrees, and a = 6, b = 7.2 and c = 8, what are [hkl]? The direction cosines are 0.3322, 0.5604, 0.7566, which are proportional to h/a, k/b and l/c. Therefore h is proportional to a*.3363 = 0.1.009. k is proportional to 3.6*.5537 = 2.0178, and l is proportional to 4*.7566 = 3.0266. Thus [hkl] = [123].

Summary:

Spherical coordinates from Miller Indices: 
    tan theta = ak/bh
    tan(phi) = ch/(al*cos(theta) = ck/(bl*sin(theta))  
Miller Indices from Spherical coordinates: 
   h = a*sin(phi)cos(theta)
    k = b*sin(phi)sin(theta)
    l = c*cos(phi); reduce to lowest terms

Hexagonal and Trigonal Systems 

For hexagonal and trigonal minerals, there are three possible axis directions, spaced120 degrees apart. We pick the 120 corner of cells rather than the 60 degree corner because this usage leads to symmetrical, consistent results. Obviously, any two intercepts specify the face, so the third intercept is not independent. Also, there will be two intercepts ofone sign and one of the other. The Miller indices for a hexagonal mineral are oftenwritten {hikl}. Indices h, i and k are related by h + i + k = 0. Some modern textsdispense with the i term and treat hexagonal minerals like all others.

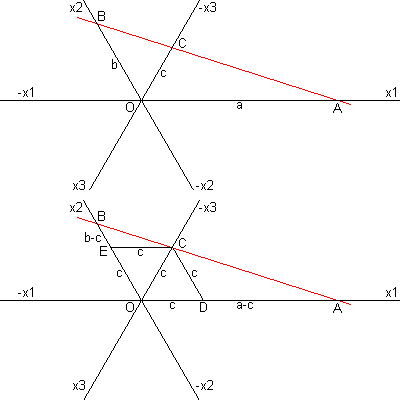The proof is simple: Imagine a hexagonal axis system as shown and a face cutting each axis with intercepts a, b, and c. Now construct CE parallel to x1 and CD parallel to x2. Obviously triangles AOB, ADC and CEB are similar. Therefore a/b = {a-c}/c = a/c -1. Dividing by a and rearranging, we have 1/a + 1/b = 1/c. Define h = 1/a, k = 1/b and i = -1/c. Then h + i + k =0. i is negative because the face cuts the negative x3 axis.

The problem with trigonal and hexagonal systems is the oblique axis system. To determine theta, we need to solve a triangle when two sides and the included angle are known. For some odd reason, there's a very simple solution that is rarely seen in math texts.

In the diagram above, u = sin60/k and also equals (v + 1/h)/tan(theta). v = cos60/k. Thus
u = (v + 1/h)/tan(theta), so tan(theta) = (v + 1/h)/u = (cos60/k + 1/h)/(sin60/k) = (cos60 + k/h)/sin60
Thus tan(theta) = (1/2 + k/h)/(√3/2) = (1 + 2k/h)/(√3) = √3(1 + 2k/h)/3 = √3(h + 2k)/3h. Note that the cell edges don't enter into it since they're both the same.

To calculate phi, we use the same approach as previously. Call the distance from the origin to the plane p (not labeled). Referring to the diagram for the orthorhombic-tetragonal-isometric cases, we have, again,
tan(phi) = ch/(al*cos(theta)). Note that for the orthorhombic-tetragonal-isometric cases, there are formulas involving a and c, and b and c. In this case we can't use the b-c formula but the a-c formula still works.

Proceeding in the inverse direction, given a, c, phi and theta, we calculate direction cosines. cx is proportional to h/a and cz is proportional to l/c. We can provisionally assume h = a*cx and l = c*cz. But cy is proportional to 1/(h*tan(theta)) or √3/(h + 2k).  Thus h = a*cx, k = h(√3*tan(theta)-1)/2, l = c*cz. Reduce h, k and l to lowest terms.

Example:

Hexagonal crystal with a = 4 and c = 7. Face [123] would classically have been written [1323] with the overhead line denoting a negative intercept, since the face cuts the negative x3 axis between the x1 and x2 axes. To find phi and theta, we know tan(theta) = √3(h + 2k)/3h =
√3(1 + 2*2)/3*1 = (5/3)√3. = 2.887 and theta = 70.90 degrees. Large values of theta shouldn't be a surprise since the cell edges are 120 degrees apart. Tan(phi) = 7*1/(4*3*cos(70.90)) = 7/(12*0.3272) = 1.783 and phi = 60.7 degrees.

Proceeding in the inverse direction, given a = 4 and c = 7, and phi = 60.7, theta = 70.9, we calculate direction cosines, which are 0.2854, 0.8241 and 0.4894, which are proportional to h/a, k/a and l/c. Therefore h is proportional to 4*0.2854 = 1.1416, and l is proportional to 7*0.4894 = 3.4258. Finding k is a bit harder. Tan(theta) = √3(h + 2k)/3h, or k = h(√3*tan(theta)-1)/2 = 1.1416*(2.887*1.732 - 1)/2 = 2.2834. We have h = 1.1416, k = 2.2834 and l = 3.4258. Reduced to lowest terms, we get h=1, k=2, l=3.

Summary:

Spherical coordinates from Miller Indices: 
    tan theta = √3(h + 2k)/3h
    tan(phi) = ch/(al*cos(theta)  
Miller Indices from Spherical coordinates: 
   h = a*sin(phi)cos(theta)
    k = h(√3*tan(theta)-1)/2
    l = c*cos(phi); reduce to lowest terms

Monoclinic System

In the hexagonal and trigonal systems, the principal symmetry axis is considered the c edge. In the monoclinic system, the principal 2-fold axis is the b direction. We'll denote the angles as ab, etc., where ab is the angle between edges a and b. Anglesab and bc are 90 degrees. Angle ac is generally not 90 degrees. If it happens to be 90 degrees, the internal atomic arrangement still lacks the symmetry to make the crystal orthorhombic. From the standpoint of geometry, it makes a lot more sense to line the twofold axis up in the z direction (the so-called "first setting") but the orientation shown here (the "second setting') is more common.

This view looks along the y axis. We need to determine the intercepts of face [hkl] in a rectangular Cartesian axis system. The y and z intercepts are b/k and c/l. We can find the third intercept much the same way we did for the trigonal-hexagonal case. The only difference is that angle ac is not 120 degrees. u = (a/h)sin(180-ac) = (a/h)sin(ac)  and u = (c/l) + v = (c/l) + (a/h)cos(180-ac) = (c/l) - (a/h)cos(ac) Note: ac > 90 so -(a/h)cos(ac) >0.

By simple proportion we have u/(c/l + v) = g/(c/l), or gl/c = ul/(c + vl) and therefore g = uc/(c + vl). We have u = (a/h)sin(180-ac) = (a/h)sin(ac) and v = (a/h)cos(180-ac) = -(a/h)cos(ac). v will still be positive becauseac > 90. Thus g = (a/h)sin(ac)c/(c - l*(a/h)cos(ac)) = (ac)sin(ac)/(ch - (al)cos(ac))

The left diagram is looking down the z axis and we can see simply that tan(theta) = g/(b/k) = gk/b. Also p = g cos(theta) = (b/k)sin(theta). The right diagram is in the plane containing the z axis and the pole to [hkl]. Obviously tan(phi) = c/pl = c/(l*(b/k)*sin(theta)) = (ck/lb)/sin(theta). Recall that for orthorhombic, tetragonal and isometric crystals we had formulas for phi that used either a and c or b and c. We couldn't use the b-c formula for hexagonal and trigonal crystals, but we can here.

We have g = ((ac)sin(ac))/(ch - (al)cos(ac)).
Thus tan(theta) = gk/b =(k/b)(ac)sin(ac)/(ch - (al)cos(ac)) = (ack/b)(sin(ac))/(ch - (al)cos(ac)).
As a check, if ac = 90, we have the orthorhombic case, and tan(theta) = ack/bch = (ak/bh).

Proceeding in the inverse direction, given a, b, c, ac, phi and theta, we calculate direction cosines. cy is proportional to k/b and cz is proportional to l/c. We can provisionally assume k = b*cx and l = c*cz. We can rearrange the formula for tan(theta) to solve for h:

h  = (ak/b)(sin(ac))/tan(theta) + (al/c)cos(ac) = a((k/b)(sin(ac))/tan(theta) + (l/c)cos(ac)). As a check, if ac = 90, we have h = ak/btan(theta). But tan(theta) = gk/b, so h = ak/b*b/kg = a/g, or g = a/h. Now g is the intercept on an axis orthogonal to b and c, and in the orthorhombic case, that intercept is also a/h.

I told you it got progressively uglier. Reduce h, k and l to lowest terms.

Example:

Monoclinic crystal with a = 4, b = 5, c = 6, ac = 110 degrees and face [123].
Tan(theta) = (4*6*2/5)(sin(110))/(6*1-4*3*cos(110)) = 9.6*0.9397/(6+12*0.3420) = 0.8928 and theta = 41.76 degrees. Tan(phi) = 6*2/(5*3*sin(41.76)) = 12/(15*0.6560) = 1.201 and phi = 50.22 degrees.

Inversely, the direction cosines relative to orthogonal axes are cx = 0.5733, cy = 0.5118 and cz = 0.6398. We have k = 5*0.5118 = 2.5590 and l = 6*0.6398 = 3.8388. h = (ak/b)sin(ac)/tan(theta) + (al/c)cos(ac)
= (4*2.5590/5)*0.9397/0.8928 - (4*3.8388/6)*0.3420 = 2.1547 - 0.8752 = 1.2795. So h=1.2795, k = 2.5590 and l = 3.8388, or, reduced to lowest terms, h=1, k=2, l=3.

Summary

Spherical Coordinates from Miller Indices: 
    tan(theta) = (a/b)((ck*sin(ac))/(ch - al*cos(ac))
   tan(phi) = (ck/bl)/sin(theta)
Miller Indices from Spherical Coordinates: 
    h = (a/b)k*sin(ac)/tan(theta) + (a/c)l*cos(ac)
    k = b*sin(phi)*sin(theta)
    l = c*cos(phi); reduce to lowest terms

Return to Symmetry Index
Return to Crustal Materials {Mineralogy-Petrology} Index

Return to Professor Dutch's Home Page

Created 26 January 2011, Last Update 11 June 2020